云风的 BLOG: 一道初等几何题

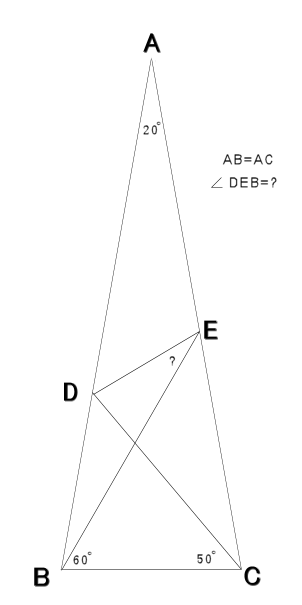
前两天看书的时候看到这道题：三角形 ABC 是一个等腰三角形，顶角 20 度。角 EBC 为 60 度，角 DCB 为 50 度。求角 DEB = ? 度。

由于是躺在床上看书，身边没有笔和纸，脑子里想不清楚，就用手机上的计算器把答案算了出来。当然，用了三角公式。结果是一个整数，这也预示着这道题很可能存在一个初等几何的解法。

一不小心把书翻了一页，看到了答案，觉得乐趣少了很多。当时觉得这是道有趣的题，就记了下来，第二天带到公司。果然，几个同事花了很长时间都没做出来 :) 到第三天才有人找到初等几何的解法。

各位观众，如果还有谁有兴趣可以一试。只需要具备初中（或仅需要小学高年级？）平面几何的知识就够了。

按书上的说法，这是一道颇为著名的初等几何题。我 google 了一下，只找到一篇相关论文：Adventitious Angles ，可惜没权限进去看。

如果实在做不出来，可以去书店在《蚁迹寻踪及其他数学探索》中找答案。这里就不公布了，否则会坏了许多人的兴致 :D

为避免 spam, 此贴于 2007 年 11 月 7 日关闭评论。想发表意见的朋友请移步留言本。

Comments

https://www.mathpages.com/home/kmath277/kmath277.htm

Posted by: 答案 | (55) May 18, 2022 12:19 PM

头一个就想到了二元一次方程。不过过程有点费劲。看来智商捉急

Posted by: swlilike | (54) June 16, 2015 09:19 AM

最简单的就是用cad做图，然后标注一下就行了。当然几何方法就是从A,D,E三点向底边做垂线，然后可以证得△adc～△bde，故∠bed=∠acd=30度

Posted by: hc | (53) August 25, 2014 01:03 PM

20°啊，30°我看了几个答案自己推导的过程都有错。。。。

Posted by: god_chun | (52) February 12, 2014 06:26 PM

虽然是07年的帖子，还是得顶一下。依稀记得在习题里面看过， 30度（三角公式，证明三角形DBE与EAB相似即可）

Posted by: venus_solar | (51) July 11, 2013 11:01 AM

Posted by: wifecooky | (50) January 14, 2013 05:01 PM

y-x=30°，我推测就是30°，验证果然正确。哈哈

Posted by: 蓝胖子 | (49) July 4, 2012 08:02 PM

5分钟不用纸币和手机就搞定。。看来我智商不比云风你低啊。。可惜我太懒了。。。

Posted by: pony | (48) September 25, 2010 12:06 AM

路过，顶一下！

Posted by: 活性氧化铝 | (47) June 5, 2009 02:28 PM

路过，踩一下！

Posted by: 聚合氯化铝 | (46) May 20, 2009 11:10 AM

180-50-(((180-20)/2-60)*2+60)=30

Posted by: Robert | (45) March 11, 2009 07:34 PM

666

Posted by: Anonymous | (44) January 4, 2009 08:21 PM

30° 因为AE=DE BD=BC 可以推出，角AED=140° 可以推出一些等比三角形。

Posted by: 令狐伯爵 | (43) December 22, 2008 08:32 PM

前次做错了...

Posted by: weifz | (42) October 4, 2008 01:29 AM

结果是45，初等几何方法做出来。用了40分钟，惭愧

Posted by: weifz | (41) October 4, 2008 01:04 AM

过E做CD平行线，交AB于F 做出平行线可以直接得到两组相似三角形根据简单比例关系计算可以发现三角形AEF全等于三角形BED 所以角BED等于脚AEF等于角ACD等于三十度。

Posted by: MGR | (40) May 24, 2008 10:58 AM

难

Posted by: Anonymous | (39) August 31, 2007 01:23 PM

到目前20，30 40度的答案都有，到底是多少度了？运风出来解释一下

Posted by: sunway | (38) July 17, 2007 05:11 PM

哈哈，看来大家的学术真高啊，这个题很简单的，相似三角形，角相等的阿，也就是AEB相似于BDE，所以角DEB就等于角BAE，等于20

Posted by: Anonymous | (37) July 16, 2007 04:47 PM

1.以E为起点，做BC的平行线，交AB于F。 2.连接CF交BE于G，交DE于H. 3。算出∠BDC=50度，推出BD=BC; 又因为三角形BCG为等边三角形，推出BD=BG,三角形BGD为等腰；推出角FDG=100度，角DGF=40度，得知三角形DGF为等腰。 4。然后证明三角形DEF和三角形DEG全等。最后角DEB=30

Posted by: Anonymous | (36) July 11, 2007 01:05 PM

我的答案是错的，应该是30度

Posted by: xiekeli | (35) July 6, 2007 08:45 PM

挺简单啊，40度呗

Posted by: xiekeli | (34) July 6, 2007 02:29 PM

挺简单，40度

Posted by: xiekeli | (33) July 6, 2007 02:27 PM

BE==AE,因为这是个等腰三角形,完了,AE+DE肯定是>AD的,因为两边之和大于第三边,得证,用了20秒想出来的,问什么需要这么复杂的解释?

Posted by: kingnd | (32) July 6, 2007 10:45 AM

哇，楼下这个网页给了一个很一般的方法来解

Posted by: nothanks | (31) July 5, 2007 01:05 PM

nnd,我做了n条辅助线。这道题的解法在这里： http://www.mathpages.com/home/kmath277/kmath277.htm

Posted by: bobo | (30) July 5, 2007 10:39 AM

这种几何证明很早就有人做了，我记得国内也有人做，具体所不清了。平面几何真是一个很奇妙的领域，现在依然记得神奇的欧拉9点圆和吓人的莫利三角。不知道这里有没有人证过莫利三角？记得当年高中的国际数学奥林匹克竞赛总共有6题，其中必有一道平面几何题。我也因此比别人多学了3年平面几何，哎，想起真有颇多感慨，当年的追梦少年现今已成一堆朽木。

Posted by: dayn9 | (29) July 4, 2007 09:46 AM

这要能写个程序解出答案就更强了.

Posted by: ix | (28) July 3, 2007 12:41 PM

Z + X = 140 (1) X + Y = 110 (2) Z - Y = 30 (3) 解得： X = 30;?? 方程（3）实际上是由前两个运算得来，实际上只有两个方程，这样本方程组有无数解 x=10;y=100;z=130 x=11;y=99;z=129 . . . .

Posted by: Anonymous | (27) July 2, 2007 07:06 AM

呵呵，正解。反过来写更清楚一些。这是我看到的第 5 种解法了 ;)

Posted by: Cloud | (26) July 2, 2007 12:23 AM

我想证明△DEF≌△DEG,依据是三边对应相等的两个△全等. 已经证明了EF=EG,而DE又为公共边,所以只要证明DF=DG即可.

Posted by: xbz | (25) July 2, 2007 12:04 AM

to xbz: EF=EG,又由于DE为公共边,只需证明DF=DG . DE 为公共边跟 DF=DG 似乎没有因果关系。

Posted by: Cloud | (24) July 1, 2007 10:52 PM

过E作边平行于BC交AB于F,连接FC交BE于G,连接DG,DE. 可以证明△FBC≌△EBC => △EFG和△BCG为等边△ => EF=EG,又由于DE为公共边,只需证明DF=DG,即可=> △DEF≌△DEG. 可以计算∠DFG=40° ∠BDC=50° => △BDC为等腰△ => BD=BC. BC=BG => BD=BG => ∠BGD=80° => ∠DGF=40° => DF=DG => △DEF≌△DEG => ∠DEB=30°

Posted by: xbz | (23) July 1, 2007 08:28 PM

yht你怎么解的方程？能得出来吗。。。

Posted by: nothanks | (22) July 1, 2007 01:48 PM

俺看了这题是先是敬仰了一下,结果1分钟就做出来了..

Posted by: Anonymous | (21) July 1, 2007 01:07 PM

令： ∠DEB = X; ∠EDC = Y; ∠AED = Z; 得： Z + X = 140; X + Y = 110; Z - Y = 30; 解得： X = 30;

Posted by: yht | (20) July 1, 2007 07:55 AM

以D为起点，做BC的平行线。角DEB为30度~~~~

Posted by: august3 | (19) June 30, 2007 11:27 PM

总算做出来了，但是还是用到了三角函数的积化和差公式，惭愧惭愧。 1.在AB上找一点F，使得BF=BE；连接EF，则∠EFB=∠FEB=80° 2.因∠DCB=∠CDB=50°,推出BD=BC 3.假设∠DEB=30°，则推出∠DEF=50°,因∠EFB=80°,故∠EDF=50°，故⊿EDF为等腰三角形，DF=EF 4.故知BD+DF=BE，因BD=BC，所以 `BD=AB*sin(10°)*2` `BE=AB/(2*cos(20°))` `DF=EF=BE*sin(10°)*2=AB*sin(10°)/cos(20°)` 5.因为 `AB*sin(10°)*2+AB*sin(10°)/cos(20°)=AB/(2*cos(20°))` 消减以后，得到 `2*sin(10°)*cos(20°)+sin(10°)=1/2` 利用积化和差公式 `sin(10°)*cos(20°)=(sin(30°)-sin(10°))/2` 又因为`sin(30°)=1/2` 故上述等式成立：`2*sin(10°)*cos(20°)+sin(10°)=1/2` 故知，∠DEB=30°成立。

Posted by: 庄表伟 | (18) June 30, 2007 11:18 PM

寻找初等几何解法的实质就是把三角函数公式化减的过程具体的画到这道题目里面。

Posted by: Atry | (17) June 30, 2007 03:00 PM

就普遍情况而言，若角 EBC 为 a，角 DCB 为 b。求角 DEB 的话，不用三角函数是求不出来的。不用三角函数要求出来的话，就必须在角的值上运用互补互余三内角加加减减。这道题的话，就必须构造一个特殊情况，让 DE 刚好出于某根特殊线上，要用已知的20度，60度和50度的关系构造出来一个特殊角，刚好等于DEB。

Posted by: Atry | (16) June 30, 2007 02:20 PM

先看了下面一个朋友的答案受到了启发,那个辅助线太多了,只要做两条就够了. 先设BE和CD的交点为G,再在BE上找一个点F,使得∠BCF=60. 易证△BDF～△ABC, 然后就算出来∠CDF=30, 再证出△DFG～△EDG, 所以∠DEG=∠GDF=30

Posted by: cat | (15) June 30, 2007 01:22 PM

俺同学看了这题也是先鄙视一下,结果还是做不出来..

Posted by: cat | (14) June 30, 2007 01:00 PM

我说错了，惭愧

Posted by: MJiA | (13) June 30, 2007 11:28 AM

抱歉，我错了，靠角度的加加减减是不行的

Posted by: Atry | (12) June 30, 2007 11:26 AM

可以根据n个三角形的关系列出一个四元一次方程，所有的根据都是内角和180

Posted by: MJiA | (11) June 30, 2007 10:56 AM

楼下差亦，3内角180度，二元一次方程怎么也只能列出一个